在分布式系统中的CAP理论中有C(一致性),大郅表示分布式系统中节点状态或数据具有一致的特性。但一致性有着不同的分类,例如常见的用于取代CAP理论的BASE中的E,最终一致性,不同于强一致性,他强调着事务最终状态趋于一致,但中间态可能不一致,利用此篇文章总结一下分布式系统的一致性分类。
根据实际系统的要求,分布式系统的一致性可以大致分为四类:
严格一致性
强一致性(线性一致/原子一致)
顺序一致性
弱一致性(最终一致性)
严格一致性
一个理想概念上的一致性,节点间数据完全一致,对外可表现为单个节点。由于网络延迟和通信等因素的存在,现实中这种一致性不可能存在。
强一致性(线性一致)
强一致性要求在全局时钟相同的条件下,对任何节点的读都相同且等于最后一次写成功的数据,这也就意味着仅仅在所有节点同步到数据后才会被标记为同步成功。
顺序一致性
顺序一致是强弱一致性的中间状态,它主要基于两种准则:
从单个处理器(线程或者进程)的角度上看,其指令的执行顺序以编程中的顺序为准;
从所有处理器(线程或者进程)的角度上看,指令的执行保持一个单一的顺序;
综合这两个约束,顺序一致性最终要求的是在不改变单个节点的指令顺序情况下,我们能够找到一个顺序组织各个节点的所有指令,使得所有指令执行结果是正确的。这样说可能比较模糊,在此引入一个示例,先是一个顺序一致性系统但非强一致性系统:
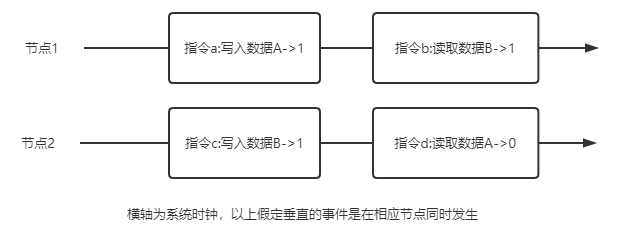
如上图,分别有两个分布式节点在两个时钟点执行了指令,如果要满足顺序一致性,我们需要保证指令b发生在a后,指令d发生在c后,而由于在指令d执行时,指令a尚未执行;指令b执行时,指令c已经执行,所以可以找到一个全局的指令顺序:
指令c 写入B -> 指令d 读取A -> 指令a 写入A -> 指令b 读取B
这一顺序是满足顺序一致性的,但如果是下图的指令则无论如何组织都不能保证顺序一致性:
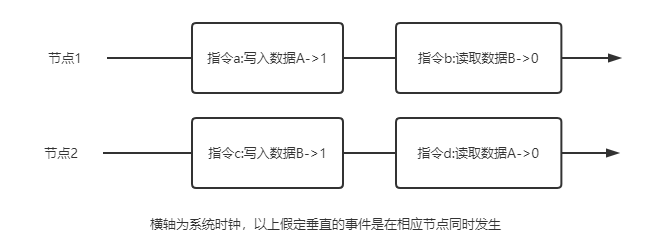
而下图则是强一致性系统,所以也必然是一个顺序一致性系统:
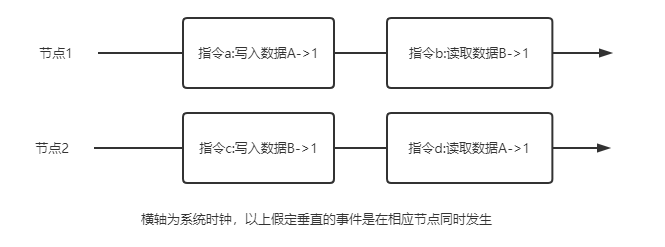
弱一致性
弱一致性是系统对强一致性的部分取舍,最终一致性就是一种弱一致性,他保证了系统最终将趋于一致并将一致,但是在一致性。例如如上图中不管哪个时钟图只要在一定时间之后AB均为1,则系统具有弱一致性。有些时候,分布式系统做出最终一致性的处理,在数据一致前,系统或数据的可用性是不能得到可靠保障的。

