前缀树(Trie,又称字典树)是一种功能倾向性很强的数据结构,通过对词汇的前缀做数结构,很容易实现查询、前缀词推荐系统,例如,我们将如下多个单词放入树结构中:
[apple,bat,bee,cat,cap,car],最终生成的前缀树结构为
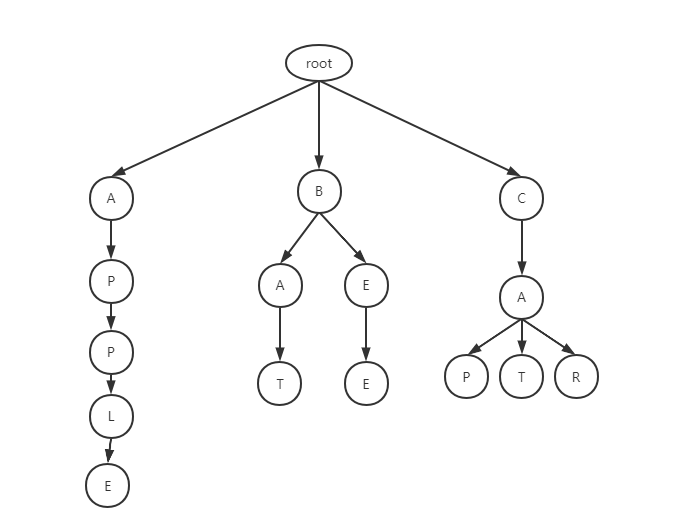
通过深度递归,我们很容易用较小的时间复杂度判断出符合前缀的单词在不在。
Trie实现1:英文单词 bucket结构
假设Trie的字符集范围是固定的,并且范围不大,例如是上面的纯英文字符,假设忽略大小写总共为26个,可以选择使用桶结构进行存储,即每一个Node都是一个长度为26的bucket数组。
public class Trie {
private TrieNode root;
/**
* 前缀树节点类
* */
class TrieNode {
// R links to node children
private TrieNode[] bucket;
//bucket长度
private final int R = 26;
//标示此节点是否包含有单词
private boolean isEnd;
public TrieNode() {
bucket = new TrieNode[R];
}
public boolean containsKey(char ch) {
return bucket[ch -'a'] != null;
}
public TrieNode get(char ch) {
return bucket[ch -'a'];
}
public void put(char ch, TrieNode node) {
bucket[ch -'a'] = node;
}
public void setEnd() {
isEnd = true;
}
public boolean isEnd() {
return isEnd;
}
}
public Trie() {
root = new TrieNode();
}
//插入数据
public void insert(String word) {
TrieNode node = root;
//循环放node
for (int i = 0; i < word.length(); i++) {
char currentChar = word.charAt(i);
if (!node.containsKey(currentChar)) {
node.put(currentChar, new TrieNode());
}
node = node.get(currentChar);
}
node.setEnd();
}
/**
* 根据前缀搜索node
*/
private TrieNode searchPrefix(String word) {
TrieNode node = root;
//循环取node
for (int i = 0; i < word.length(); i++) {
char curLetter = word.charAt(i);
if (node.containsKey(curLetter)) {
node = node.get(curLetter);
} else {
return null;
}
}
return node;
}
/**
* 搜索是否存在指定的前缀,非完全匹配
*/
public boolean startsWith(String prefix) {
TrieNode node = searchPrefix(prefix);
return node != null;
}
/**
* 搜索是否存在指定的词汇
*/
public boolean search(String word) {
TrieNode node = searchPrefix(word);
return node != null && node.isEnd();
}
}
这样看来,Trie的结构并不复杂,只通过循环不断提高深度进行遍历即可。
Trie实现2:字符集未知,Map结构
假定字符集的范围是未知的,或者范围很大(比如中文汉字),就要放弃使用bucket结构,而是通过一个Map维护,这里使用树结构TreeMap,key为相应节点的字符。
public class Trie {
static class TrieNode {
char c;
int occurency = 0;
TreeMap<Character, TrieNode> children;
public TrieNode() {
}
public TrieNode(char c) {
this.c = c;
}
}
TrieNode root;
public Trie() {
root = new TrieNode();
}
public void insert(String word) {
insert(word, root);
}
/**
* 将从index处开始的字串插入到root的子节点中,即将index对应的字符插入到root的子节点中
* @param word
* @param root
*/
private void insert(String word, TrieNode root) {
TreeMap<Character, TrieNode> children = root.children;
for(char c :word.toCharArray()){
if (null == children) {
children = new TreeMap<>();
root.children = children;
}
if (!children.containsKey(c)) {
children.put(c, new TrieNode(c));
}
root = children.get(c);
children = root.children;
}
//标识此位置有完整单词匹配
root.occurency++;
}
public boolean search(String word) {
return search(word, root, 0);
}
/**
* 在root的子节点中搜索从index开始的字串
* @param word
* @param root
* @param index
* @return
*/
private boolean search(String word, TrieNode root, int index) {
assert index > -1 && index < word.length();
char cur = word.charAt(index);
if (root.children == null ||
!root.children.containsKey(cur)) {
return false;
}
if (index == word.length() - 1) {
return root.children.get(cur).occurency > 0;
}
return search(word, root.children.get(cur), index + 1);
}
public boolean startsWith(String prefix) {
return startsWith(prefix, root, 0);
}
/**
* 在root的子节点中搜索从index开始字串对应的前缀
* @param prefix
* @param root
* @param index
* @return
*/
private boolean startsWith(String prefix, TrieNode root, int index) {
assert index > -1 && index < prefix.length();
char cur = prefix.charAt(index);
if (root.children == null ||
!root.children.containsKey(cur)) {
return false;
}
if (index == prefix.length() - 1) {
return true;
}
return startsWith(prefix, root.children.get(cur), index + 1);
}
}

