接雨水问题
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。
预热1
木板组成水桶装水，定义高度为一数组，间隔为1，求水桶最大容量如[1,5,1,2,6,3]为15，解题思路：自两边木板向中间遍历求容量，每次相对短的木板向内移动，共比较n-2次。
解析1
将水灌满，求灌满后的高度，其实就是从最高点向左右两个方向向中间遍历，依次求经过的最大值，这样一来就是从最高点向两侧递减的，再减去柱子原高度即可。
public int trap(int[] height) {
if(height == null || height.length <= 2)
return 0;
int maxL = height[0];
int[] maxRs = new int[height.length];
int waterSum = 0;//计算总的水量
int maxR = 0;
for(int i = height.length - 1; i >= 0; i--){
if(height[i] > maxR) {
maxRs[i] = maxR = height[i];
}
else {
maxRs[i] = maxR;
}
}
for(int i = 1; i < height.length - 1; i++){
if(height[i] > maxL) {
maxL = height[i];//更新左边最大值
}
waterSum += Math.max(Math.min(maxL, maxRs[i]) - height[i], 0);
}
return waterSum;
}
容易理解的想法还有按高度分层计算，但是时间复杂度过高。
进阶1
拓展到二维数组，这一题的解法会变得异常困难：
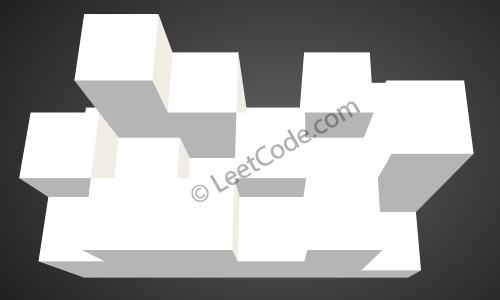
如上图所示，这是下雨前的高度图[[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] 的状态。
2019-03-14Sherlock